
RNG Quality assessment
A timely article flew by on Reddit about the
RANDU pseudo-random generator algorithm widely used in the 1960s, which it turns out was very flawed indeed. It was explained to one student that ''We guarantee that each number is random individually, but we don't guarantee that more than one of them is random''. Basically it produced numbers that belonged to one of 15 "planar" groupings and nothing in the gaps between the planes. It isn't just a minor annoyance, because many statistical studies in the 60s and 70s used it, and it can easily have contaminated their results. That's definitely not what I am trying to reproduce with the ring oscillator device -- so how can I figure out how "good" the randomness is in an objective way?
RNG quality test suites
It turns out that empirically testing RNG outputs has been the subject of a lot of work for decades, and there are some established testing suites available online. A major one seems to be the "
diehard" suite -- I guess it is a pun on die as the plural of dice.
It needs you to fetch 10M bytes of random numbers or more and let it run a bunch of tests on them. The output was a little hard to assess initially: most tests issue a "p" number which only suggests something is bad if it is 0.000... OR 0.999.... All other numbers inbetween are to be taken as a good result as I understood it. Except there is a warning that even good RNGs can produce the occasional test fail.
Thus you should not be surprised with occasional p-values near 0 or 1, such as .0012 or .9983. When a bit stream really FAILS BIG, you will get p`s of 0 or 1 to six or more places. By all means, do not, as a Statistician might, think that a p < .025 or p> .975 means that the RNG has "failed the test at the .05 level". Such p`s happen among the hundreds that DIEHARD produces, even with good RNGs. So keep in mind that "p happens"
I duly fetched 10M bytes of 115kbps randomness from the device and fed it to diehard. It seemed to give fine results except on "Count the 1s stream" and "Squeeze" (devastating p=0.000000), "Count the 1s specific" for bits 1-11 (p=0.000030) and 9-16 (p=0.000064), and QQSO 2-6 (p=0.000005). It passed the dozens of other tests but it was disappointing, looks like a big fat 'failed'.
Triple Scoop
Well, since my test CPLD was an XC95288XL with 288 Macrocells to burn, I naturally wondered if I could improve matters by tripling the amount of ring oscillators getting Xor-ed -- that is to implement the three varying sized oscillators 3 times each, totaling nine, and sum them with a big XOR. They'll all be drifting around individually as much as together, it should be a mighty noise-fest.
I edited the VHDL and blew it into the CPLD... visually the summed RNG output "bit" was an awful lot more noisy than before. I pulled another 10M bytes from that setup: but just looking at the byte distribution as I did before told me something is still up.

That sawtooth type distribution is "not random" to coin a phrase. If you look at the large jump at 0x80 (128) it is telling us that we are more likely to get 1000000 binary than we are to get 01111111, in other words, since this is over 10M bytes, there is a distribution problem favouring '0'. When I analyze the distributions of 1s and 0s I find
0: 40436204, 1: 39563804... delta=872400, skew=1.090500% |
You can see the same thing even better looking at 0x00 (42,000 hits) vs 0xFF (36,000 hits), they are like 8% off the median of 39,000. Clearly that distribution of 1s and 0s has to have a very small skew to stop these kinds of effects showing up, and equally clearly this is telling us something deep about the RNG hardware.
Spiky
Although the individual oscillators are quite slow thanks to the number of inverter stages, at 4 - 6MHz, the way they are being summed makes for trouble from bandwidth limitations inside the CPLD. At the moment it just uses a dumb asynchronous XOR action, that means that potentially very fast spikes can be seen when one "slow" oscillator changes state very shortly after another "slow" oscillator. For example:
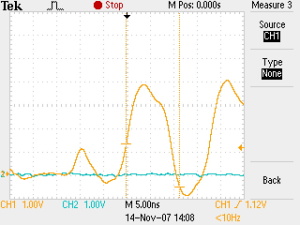
You can see on the left (this is 5ns/div notice) a runt pulse where this happened, the XOR was convinced to rise by one oscillator changing and then countermanded when another oscillator changed state less than 5ns later, resulting in a doubtful pulse that was probably not visible as a '1'. This also happens when going from '1' to '0', but maybe the threshold for the transistors in the CPLD is not at exactly 50% of the 3.3V supply. So we suddenly have it seeing more '0's than '1's on average when spikes are involved.
This whole high bandwidth summing step is completely needless, it's only there because it is a literal interpretation of the diagram in the original RFC. I changed it instead to have nine latches sample the nine oscillators every 125ns (there is an 8MHz clock on the prototype board) and sum those results with XORs into a single bit. In turn this output is sampled by another latch at 8MHz to hide any metastability.
Latched up
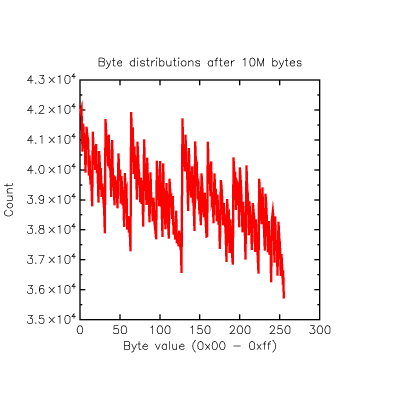
The latched summing version performs much better and has gotten rid of most of the bit skew, and the sawtooth behaviour:

...but there is still a problem with 0x00.... the bit skew looks like this
0: 39960076, 1: 40039932... delta=79856, skew=0.099820% |
so the skew is now on the side of '1's but only by 0.1%. You can see the byte count spread is much tighter than before too -- 1800 instead of 6000 counts before.
Balancing out the skew
Well if the remaining skew is something to do with the ratio of rise to fall times, or the non-squareness of the oscillator outputs for some other reason by something as low as 0.1%, that is hard to do much about, especially as it may vary on the specific silicon die.
But it shouldn't matter -- now the bandwidth situation at the XOR summer is sane, if we invert the summed output 50% of the time it should spread any excess on '1's or '0's to the opposite as well, cancelling any bias. I added a couple of terms to the summer to xor against the UART bit index LSB and a bit which toggles after every byte sent by the UART. It's the equivalent of xor with 0x55 for the first byte and then 0xAA for the second byte, over and over.
That glitch in the middle is actually at 134 (0x86), maybe it is random but I guess we will see.... the skew is further reduced as anticipated
0: 39974218, 1: 40025790... delta=51572, skew=0.064465% |
Diehard sequel
I ran 10M bytes from this version through Diehard again... the really bad p-value results are gone. For example Squeeze was a deadly 0.000000 before and is now 0.255260.
I made one last adjustment, I added the current state of the latched random value to the XOR term. That means it decides whether to keep or invert the latched value, it no longer directly accepts the value from the RNG. This got me to the promised land: 0.0005% skew between '1' and '0'.
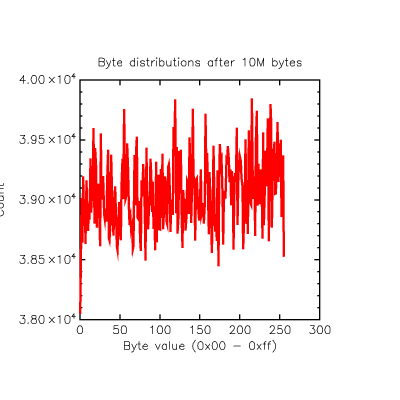
0: 40000206, 1: 39999802... delta=404, skew=0.000505% |
This also gets me the apparently good diehard results with no obvious failures on any tests, you can see the actual results
here. So it seems the current version can tentatively be called a "real RNG".






