Pretty random
After some scrabbling around porting my Jtag SVF interpreter to Octotux and creating a kernel module for the PIO end of it -- and moving to a different board with a XC95288XL CPLD to prototype it, the triple ring oscillator RNG is working. It issues a 9600 baud result, but after some initial confusion I modified it 1/8th of the time to sit out a sample time leaving "break" on the serial line. This should make sure that the receiving UART does not get confused by the data as a start bit. The true data rate is something like 800 random bytes per second at 9600 baud.
Here are the three chains of inverters (19, 23 and 29 long) oscillating at the different fundamentals
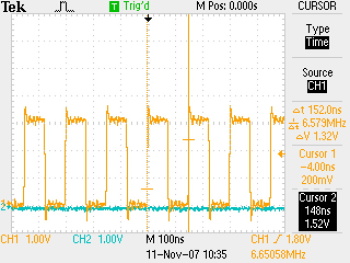
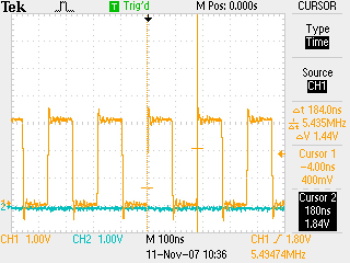
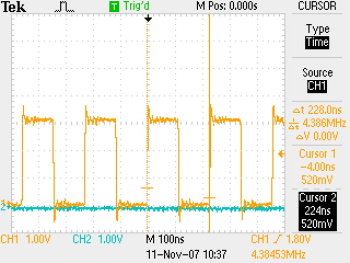
... and here is what the xor summing looks like, first over 1s then sampled once.
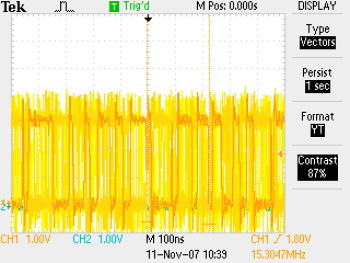
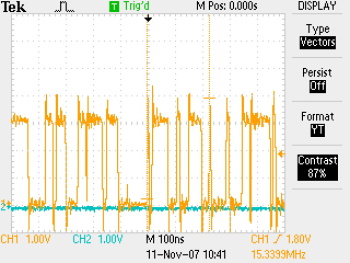
Although the single shot sample doesn't look very random, the oscillators are drifting around all the time. If you wait a little while between samples (currently it is 104us, a 9600 baud bit-period) it's pretty hard to guess what phase all the oscillators have drifted to -- at least, that's the plan.
Distribution of binary levels
The first test I did was to see what the distribution of '1' and '0' in the results was... clearly if the device is really random it should on average be 50% each. I fetched 1M random bytes, or 8Mbits:
| 0: 4008913, 1: 3991095... delta=17818, skew=0.222725% |
Its okay for a really random source to deviate to 50:50 at any given time, although on average it should be 50:50.
Octet distribution
Next I looked at the distribution of the results from 0x00 through 0xFF as the result "random byte". This would show up if the RNG fails to ever issue some result or favours certain results over others -- every result should on average have an equal chance of showing up and so an equal count. I ran it for 1M random bytes...
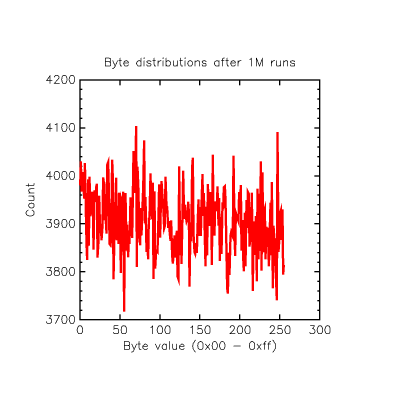
This is pretty decent, every possible result is seen with a frequency within +/-200 counts of the 3,900 average after 1M bytes.
115200 baud results
Encouraged by this I cranked the baud rate up to 115220 or 8.68us between samples and around 10K random bytes per second. The skew is increased somewhat and the spread of result counts is increased a little.
| 0: 4028746, 1: 3971262... delta=57484, skew=0.718549% |
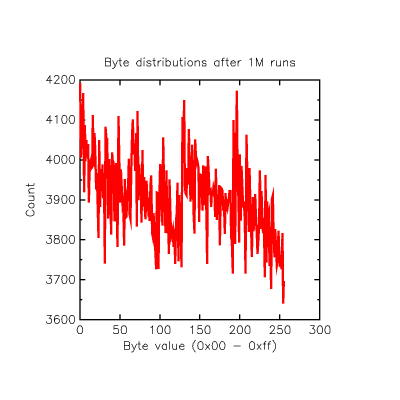
So far so good!








