The magic code project has gained a name and there are some new results to share.
The full sources for the experimental modem using the correlator codes is available at
http://git.warmcat.com under GPL2+ license.
The big change is what I call "scrambling". The 126-bit magic correlator sequence is disordered and xor-ed in 258 random ways,which are selected to not correlate well with each other at any offset (less than 43/128 match). This allows us to issue whole bytes in one code by selecting which disordered correlation code to transmit. The other two codes are for start and end of packet markers. I first tried 22 scrambles to allow 4 bits per code and some extra codes, this worked fine but I was able to extend it to 258 without really damaging the "best" scramble-scramble false correlation score too much.
The gain here is that the self-ordering and threshold properties of the code now reaches up to entire bytes: you always get a clean, aligned byte or you don't get anything: with high probability you don't get a wrong byte.
I also changed the demodulator code to something that is currently quite expensive to run. Instead of tracking a reference phase at the receiver, which is tough to do in the presence of extreme noise and phase wrapping, at each sample it tries to demodulate using that sample as "0 degrees" and a 50% phase slicer to get the bits. It's expensive because it has to do that against each of the 258 scrambles every sample -- but on the plus side the correlator does not run
at all for 124 symbols out of 126 (98.4% of the time) after there has been a successful decode, since it knows it is partway through a 126-symbol code. Still the number of demodulation attempts can definitely be reduced, maybe by subsequently just doing it on the last winning phase and a few either side.
I found that the noise performance of the demodulator is strongly dependent on the relationship between the sample rate and the carrier frequency. It's much less dependent on the number of carrier cycle periods per symbol, so long as you have 4 or 5 or above (2 works but is killed by hardly any noise). Since there is plenty of filtering to the carrier going on I didn't really expect that. Here is a graph of the noise performance when there are 96 samples per carrier (48kHz sample rate, 500Hz carrier, 100baud -- these are intra-code symbols, it's 6.25bits/sec effective):
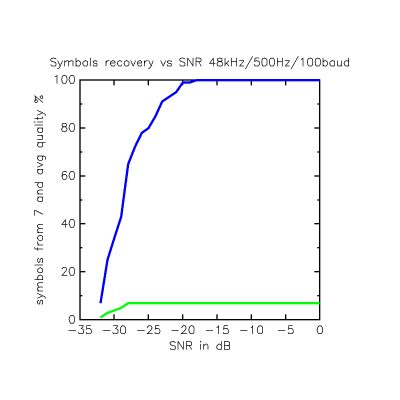
The noise performance doesn't look too bad, at least with these synthetic tests and unrealistic 48kHz sampling. It can recover all 7 bytes that are sent even at -28dB, when only 4% of the received power is the signal and the rest is white noise. And because of the code properties, these are definite bytes being captured with quite high probability, not the kind of uncertain decode that would normally be expected in such noise.
The "average quality %" shown in the graph is the percentage of demodulated bits in the matched code scramble that actually were "right", averaged over all the bytes. If a byte is missing because its quality was below the threshold of 70/128, it counts as 0% quality. Up until -20dB, the demodulator is doing well and the recovering individual bits almost perfectly. Without the Correlator code, after -20dB you would be dealing with a rapid increase in bit errors from the demodulator and relying on ECC. By using the Correlator coding though, we are able to push performance another 8dB into the noise (we even recover half the symbols at -30dB, or 10dB further) and still maintain the alignment and high probability of correct decode advantages.
This shows the effect of keeping everything else the same, but bringing the sample rate down to 8kHz from 48kHz
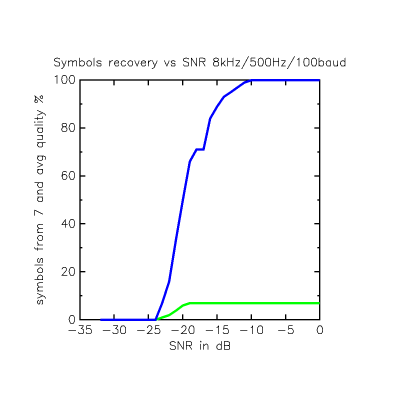
You can see the BPSK demodulation starts to fail at -10dB instead of -20dB and the correlation code again buys you another 8 - 10dB into the noise after that.
Here is the spectrum after bandpass and lowpass filtering that is actually "transmitted", the peak is the carrier at 500Hz in this case.
Another aspect of this setup is that although the demodulator is currently pretty expensive in CPU (and power), the modulator is much simpler. It just requires a 1KByte table for the scrambles and a precooked integer sine table if you are running a separate carrier than the RF one itself. Then it just needs enough logic to walk through the scramble table entry at the symbol rate (and the sine tables at the sample rate if you're using it). That can fit in part of a tiny flash controller, using a 1-bit output of a shifter to switch the phase of the transmitter. It can be simplified even further by not using scrambles but just sending a bit per code sending the code forwards or backwards to signal a '1' or '0'.
It seems that I can begin to understand where this system fits into the existing high noise codings already used by ham radio folks. The correlator code is a special case of using an ECC code, in this case where 8-ish bits are exploded into an 126-bit "space" filled with correct decodes, damaged but recoverable decodes and invalid decodes. The error correction performance of adding 8-10dB "coding gain" is probably a bit (not so much, from what I can work out) poorer than an optimal use of 126 bits to code for 8, but the advantages that attracted me to the code in the first place can offset that for some applications, the guaranteed self alignment right down from demodulation to byte boundaries, and a quite firm decode success threshold. In addition, it seems some of the more optimal decoding schemes for stuff like Viterbi can be very compute-intensive, whereas although at times we do a lot of it, the correlation action is simple and lends itself to being done in parallel. Turbo codes are patented. So it's not a one size fits all technique, but it has its niche.
I guess the next stage is looking to BPSK modulate and recover an RF carrier directly, but that will need some thinking on because it will be a very frequency-specific design, unlike these baseband tests where you can just edit the important variables and recompile. For example if it can be done initially at the UK 40MHz ISM band it will be possible to consider logic looking at carrier zero-crossings for phase assessment easily enough, and to autocorrelate just the averaged recovered phase at 4 times the symbol rate.
