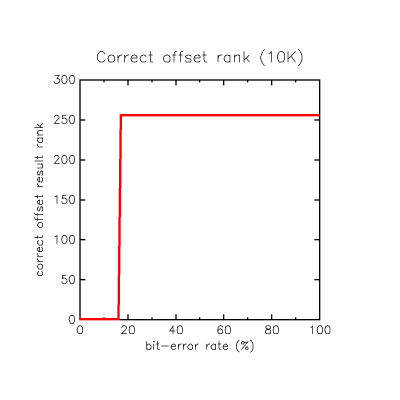
Well, the first cut of the QPSK demodulator, bit slicing and correlation code works, and this stochastic performance graph sums it up.
It shows 1,000 Monte Carlo runs each from 0% to 100% noise on the raw channel, considering correct correlator matches only, the blue line shows the WORST correlator match result at that noise level, the red line is the BEST correlator result seen at that noise level, and the purple line is the mean correlator match result seen at that noise level.
The Green line is the +64 threshold as a reference... below this we don't consider the correlator to have matched, something we chose based from studying the code response to noise a couple of posts ago.
Basically it shows that up to about 20% channel noise there is a very strong probability we return perfect results (+128 result means that no bit errors were present in the recovered correlator code).
After that there is a region up to about 50% noise where perfect results are sometimes seen, normally there is some corruption, but on average we can still recover a corrupted but high probability correctly sync'd code (whether the attached data payload can survive that beating is another issue... we can at least have reasonably correct bit-sync to whatever is there, allowing payload averaging for example).
But after 60% noise, the probability of finding a usable recovered code is less than 1 in 1000.
If you consider the purple mean line as the overall average recovery capability, it's clear that
at the moment after 40% noise things stop being much fun.
These figures reflect the whole reception system: at the moment the data slicer is a primitive edge-triggered type thing, pretty sure that is the limiting factor here. When I eyeball the recovered data payload when it is challenged by heavy channel noise, It is often broken in a "sticky" way:
hello magic code
hello ma--------------------------
hello magic code
gllo magic co$------
hello magic code
--------------oo magic code
hello magic code
Yello magic co------7
hello magic code
hello magic cod
I think the sequential bit errors will be harder to create if a more robust bit-slicer is figured out. Here is an idea of what 45% noise in the channel looks like:
and what happens to that nice clean, digital-looking demodulation when you give it that instead of the nice clean sine waves:
That last one is the input into the bit slicer, which has the job of choosing where the bit boundaries are... at the moment it looks at zero-crossings, if it were possible to do a more sophisticated job than that a lot more packets could be saved you would think. I have an extremely cool idea about this I will look into next.
