Looking at weak signal capture at the moment, there has been considerable work done on this by Radio hams. The extreme cases for these guys are bouncing signals off the moon or meteors to reach other places on the planet. The most recent protocol I could find is called
JT65, and it makes some pretty extraordinary claims for data recovery: 100% recovery at -27dB SNR, ie, the noise floor is 27dB above the signal. Unfortunately it seems the author of this otherwise cool and interesting protocol took it a step too far, and used
"forbidden Black Magic" in his implementation to get results at that level.
However removing the black magic the claim of 100% recovery at -22dB SNR using another "forbidden" but less magical technology is not being disputed. This is a patent-encumbered "soft" Reed-Solomon decoder which is able to recover from more damage faster than the normal "hard decision" decoder: this means you have to give up another few dB to get a distributable implementation. An open source implementation exists at
berlios but it's written in freaking Fortran. Multithreaded Fortran with a Python GUI. This provides a normal Reed-Solomon FEC implementation which is used if you don't have the external forbidden one.
One awfully limiting "trick" and two really interesting techniques are used in the protocol. The bad news is that very very long symbol-times are used for transmission, 372ms per 6-bit symbol. Considering the various bloatages it's about one byte per two seconds. They are sending one of 64 "tones" to encode the six bits during that time... obviously the symbol duration helps with recovery. This "trick" is the core feature of weak signal recovery... repeat what you are doing a lot, in this case repeat the "tone" cycles a lot to "amplify" the signal at a receiver which knows how to take advantage of looking for something happening multiple times to increase probability of detection.
The first interesting trick is just the amount of Reed-Solomon used... this is not new to me since I used it as part of Penumbra. But in this protocol, every 72-bit packet has an additional 306 bits of error correction attached to it :-O. That's more than 4 times as much ECC as data, and despite that it still pays off for capturing the signal.
The second cool technique is to interleave the payload data with a binary autocorrelation "clock". Since the noise level is so crazy, it's of little use to expect a 1-bit channel in the data to be usable as a "start of frame" marker or somesuch as you would normally expect with digital serialized communication. Instead, they spread the sync information in this interleaved "channel" using a 126-bit sequence which has a magically cool property... if you autocorrelate the sequence with itself, even in the presence of a fair bit of noise, every correlation offset except the right one matches MUCH worse than the 1:1 lineup. Here is the sequence extended to 128 bits and correlating with itself. The y axis is the number of bits that match.... obviously that is 128 when it compares itself to itself at the 0 offset on the X axis. The cool part is how low the self-correlation is everywhere else, no better than 20, or a 14dB "SNR" between a match and a non-match.
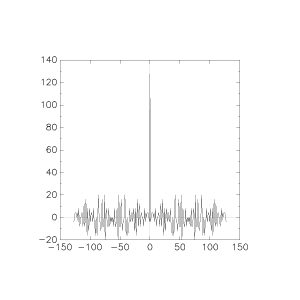
This remains the case even under pretty bad noise, up to 25% of the bits being trashed (still 9dB sync SNR):
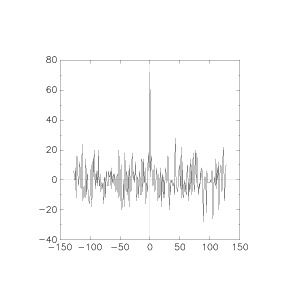
but at 30% of the bits being trashed, the performance falls off a cliff:
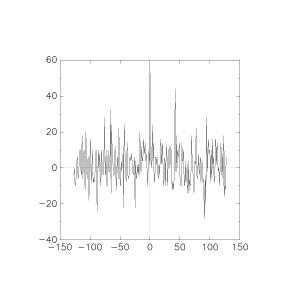
Not only does the noise floor rise due to falsely improved correlations, but the one true correlation is also falsely degraded. After about 28% bit errors the reliability is gone. (Note the noise is one-shot with the test program, rather than being Monte Carlo'd, but I ran it several times and the graphs shown are representative).
But that isn't the end of the story for this code. First the correlation action is a filter for transmission presence all by itself. And if you detect the transmission by the presence of the correlation code, you have also sync'd the receiver to the transmitted frame, since the correlation bits are interleaved with the actual data and the "0" offset marks the start of the frame.
With deep memory and a known period of retransmission from the source, temporally averaged autocorrelation can take place to increase the chances to find the presence of a transmitter and to sync up to its data. After a transmitter "sync" has been found in the averaged data with high probability, the averaging memory can be turned to only store the times when a transmission was expected from the known schedule of the transmitter.
Here is the magic code with the 128-bit sequence and the test loops
#include
static unsigned int u8Auto[] = {
0x19, 0xbf, 0xa2, 0x89, 0xf3, 0xf6, 0x58, 0xcd,
0x2a, 0x81, 0x01, 0x4b, 0xab, 0x4c, 0xc2, 0xbf
};
#define AC_LEN 128
char GetAc(int n)
{
n = n & (AC_LEN - 1);
return (u8Auto[n >> 3] >> (n & 7)) & 1;
}
int main(int argc, char ** argv)
{
int n, n1;
int nSum;
int nNoise = 0;
int nSeed;
FILE *f = fopen("/dev/urandom", "r");
fread(&nSeed, sizeof(nSeed), 1, f);
fclose(f);
srand(nSeed);
if (argc == 2)
nNoise = (1024 * atoi(argv[1])) / 100;
fprintf(stderr, "Noise: %d%%\n", nNoise);
for (n = -(AC_LEN - 1); n < AC_LEN; n++) {
nSum = 0;
for (n1 = 0; n1 < AC_LEN; n1++) {
char c = GetAc(n + n1);
/* simulate white noise */
if ((rand()&1023) < nNoise)
c = c ^ 1;
if (GetAc(n1) == c)
nSum++;
else
nSum--;
}
printf("%d %d ", n, nSum);
}
return 0;
}
and the graph command that generated the graphs (the 28 is the percentage of noise to graph)
gcc test.c -o test ; ./test 28 | graph -Tpng --bitmap-size 1200x1200 -FHersheySans>temp.png && convert temp.png -scale 300x300 png:temp1.png
